Has Hawking Explained God Away? God, Physics and the Beginning

Some naturalists have argued that the progress of science has worked to strip away God’s role in the world. Cosmologies in which the universe does not have a beginning seem to undermine the doctrine of “creation ex nihilo”; some cosmologists have even claimed that our universe could spontaneously have begun to exist out of nothing (Krauss, 2013). Multiverses are used to explain the order and structure of our universe, removing the need for a designer.  This article examines such arguments by examining the popular writings of Stephen Hawking.

A Rough Guide to The Hartle-Hawking Model
Does the Hartle-Hawking Model Avoid a Beginning?
Does This Universe Need a Cause?”
The Design Argument and Hawking’s Grand Design

1. The Hartle-Hawking Model

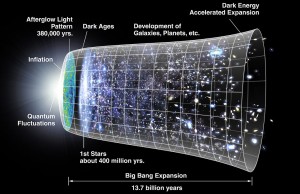
According to the standard big bang hypothesis, the universe came into existence a finite time ago. The overall theory within which the hypothesis is formulated is general relativity. The standard big bang hypothesis says that the universe emerged from singularity at which  the space-time curvature was infinite and matter was compressed to an infinite density.  We cannot continue to apply our   relativistic cosmological theories beyond this point because equations break down when a physical theory contains an infinite quantity. Stephen Hawking categorically states that at the initial ‘singularity’ the laws of physics break down

A singularity may be regarded as a place where there is a breakdown of the classical concept of space-time.  Because all known laws of physics are formulated on a classical space-time background they will break down at a singularity.  This is a great crisis for physics because it means that one does not know what will come out of a singularity. (Hawking, 1976, p.)

The big bang hypothesis does , then, provide empirical evidence for the claim that the universe began to exist.

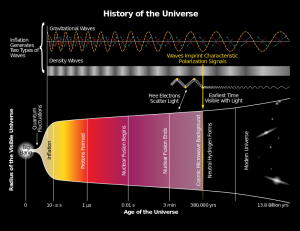
However, general relativity may not be applicable to the very earliest era of our universe. Davies notes a “rule of thumb” used by physicists. If a theory has no inbuilt unit of length there is no way to predict when the theory will break down., Newton’s gravitational constant G can be combined with Planck’s constant h and the speed of light to make a quantity with a unit of length known as the Planck length  which is about 10^-33cm. Dividing the Planck length by the speed of light we get the Planck time which is roughly 10^-43 seconds. Davies notes that “..the Planck time serves as a warning: we should not trust general relativity when extrapolated to within one Planck time of the origin” (Davies, 2006, p.86).

Einstein’s general theory of relativity fails to take into account the quantum fluctuations which must be present in any physical process involving gravity; therefore  general relativity cannot be extrapolated in an unmodified form to predict what will happen at or below the Planck length. Quantum fluctuations also affect our measurements of time. The simplest way to define a unit of time is to measure the interval it takes for a swinging pendulum to complete a full oscillation. However, we cannot measure the precise location of the pendulum (Lidsey, 2000, p.118-119). The terms “space” and “time” do not have an adequate physical meaning below the Planck limit because neither can be measured.

Such considerations led to the development of quantum cosmology:

First up was John Wheeler in the 1960’s who argued that quantum uncertainty would fuzz out the singularity, replacing the infinite curvature of space-time….One way to see this is to compare the singularity to the point of an infinitely sharp needle. Quantum mechanics applied to a real needle would make the position of the tip slightly uncertain, in effect blunting it. Will quantum mechanics blunt the space-time singularity that may have bounded the past of our universe? (Davies, 2006, p.86)

Of course, the difficulty with this analogy is that needles are within space-time  whereas quantum cosmologists are trying to explain the nature of space-time itself. A further problem arises in giving the quantum state of the universe. Quantum mechanics describes how an electron orbiting a proton in a hydrogen atom possesses only discrete energy levels. These levels start at the lowest energy configuration – the ground state – and continue in an ever increasing number of exited energetic states. One cannot determine the behaviour of a hydrogen atom if one cannot specify its initial state. If it is in an energetic state it will jump to the ground state and emit one or more photons. If it is in a ground state it will remain there.

The electron could be in any one of an infinite number of superpositions of energy levels. The same is true of the universe.  It was difficult for quantum cosmology to give an adequate description of the universe  because the universe could be in any one of an infinite number of quantum states and different results follow from each state. However, in the early 1980s Hawking and Hartle suggested that the universe might be a “special ‘natural’ quantum state – a sort of ground state “(Davies, 2006, p.87). They postulated a quantum mechanical wave function for the entire universe, using Richard Feynman’s “sum over histories” formulation of quantum mechanics (Holder, 2004, p.58). This can be applied to the universe as a whole to describe the evolution of its whole spatial geometry.

Feynman’s approach is to find the probability for a certain final quantum state by a path integral, a “sum over histories.” In quantum terms, this is a superposition of states. Every possible universe history is part of the wave function; each possible end state has an associated probability of realization… (Craig and Sinclair, 2009, p.177).

Hartle and Hawking used Euclidean metrics to describe the earliest phases of the universe’s existence. Euclidean metrics treat the time dimension as a spatial dimension. Time in the period before 10^-43 seconds can only be described with the use of imaginary numbers which are multiples of.  In the earliest epoch space and time are treated as one four dimensional Euclidean space. This four-dimensional space is finite in size and has no boundary or edge. So, in this “no-boundary” model, there is no need to specify a boundary condition to calculate the evolution of the universe.

Davies gives a “rough picture” of the Hartle-Hawking state:

A key feature of the chosen state is the way quantum uncertainty ‘fuzzes out’ space and time. Applied to a particle such as an electron, quantum uncertainty implies that its position and motion are somewhat ill-defined. Applied to space-time, quantum uncertainty means that space and time themselves are somewhat ill-defined: points in space get smeared, moments in time get smeared. But more than that, quantum fuzziness entails smearing the separate identities of space and time….Sometimes intervals of time behave like intervals of space and vice versa. The resulting identity crises –quantum fluctuations in spaceness and timeness are exceedingly small: in fact they are more or less restricted to Planck lengths and times (Davies, 2006, p.87).

The universe does not contract back to a radius of zero at a certain predicted time; rather time begins to adopt space like qualities at about one Planck-time. Time does not change abruptly into space but gradually becomes purely space like. At the beginning of the universe there were four dimensions of space, one of which was transformed into time. When the universe became larger at 10^-35 seconds the quantum fluctuations associated between time and space became negligible and space and time took on separate identities. This “switching on” of time, however, did not happen in one well defined instant. The universe did not originate from a singularity. (Davies, 2006, pp.89-92).

 2 Does the Hartle-Hawking Model avoid a beginning?

Hawking has argued that this model leaves no room for God:

So long as the universe had a beginning we could suppose that it had a creator. But if the universe is really completely  self-contained, having no boundary or edge, it would have neither beginning nor end; it would simply be. What place, then, for a creator? (Hawking, 1998, p140-141)

However, it is not at all clear that the Hartle-Hawking model gives a intelligible physical description of the early universe. The difficulty lies in giving the concept of ‘imaginary time’ a realistic interpretation. Copan and Craig ask “[w]hat would it mean to speak of a lapse of an imaginary second or of a physical object’s enduring through two imaginary minutes?” (2004, p.236).  And Hawking himself states:

Imaginary numbers can be thought of as a new kind of number at right angles to ordinary real numbers. Because they are a mathematical construct, they don’t need a physical realisation; one can’t have an imaginary number of oranges or an imaginary credit card bill. One might think this means that imaginary numbers are just a mathematical game having nothing to do with the real world (Hawking, 2001, p.59).

Furthermore, imaginary time obscures the difference between past, present and future. Time is metaphysically distinct from space: we should be able to order its moments  into “earlier than” and “later than” relations. However, Holder (2004, p.60) and Copan and Craig (2004, p.236) note that these problems can be avoided if we do not interpret the Hartle-Hawking model realistically.

Physicists can treat time as a spatial dimension to solve certain problems in quantum mechanics. This is merely a calculating device, and carries no ontological commitments. Physicists normally reconvert to real numbers. If we do this with Hawking’s model, the singularity reappears (Copan and Craig, 2004, p.237). Indeed, Holder notes that Hawking does not seem to interpret his model realistically in his technical papers:“one is left wondering, with Quentin Smith, whether Hawking is wanting to ‘baffle and intrigue’ his popular audience when those writings are in flat contradiction to his technical papers” (Holder, 2004, p.61).

However, it is possible to give this quantum gravity model a physical interpretation which supports the idea that time had a beginning. Prior to the Planck time, the model posits a finite, imaginary time on a closed surface. The model avoids a singularity with infinite physical qualities. There is no definite point of creation; however, having a beginning does not entail having a definite beginning point. For any temporal interval in the universe, the Hartle-Hawking model entails that there are only a finite number of equal temporal intervals earlier than it (Copan and Craig, 2004, p. 235-236). Bradley Monton agrees with Craig that something can begin to exist without having a definite first moment of its existence:

That is, it could be the case that the set of times at which the universe exists is open at the beginning. In other words we could pick a coordinate system with the following result: the universe does not exist at t=0, but the universe exists at every moment t>0. I maintain that, if the big bang theory is true but the universe did not have a first moment of its existence, it nevertheless began to exist, because it has only been in existence a finite amount of time (Monton, 2009, p.96).

The Hartle-Hawking model fails to give us any reason to believe that the universe did not have a beginning; furthermore“… the use of imaginary quantities for time is an inherent feature of all quantum gravity models. This precludes their being construed realistically as accounts of the origin of the space-time universe in a timelessly existing four-space” (Copan and Craig, 2004, p.237)

3. Can the universe begin to exist without a cause?

However, even if quantum gravity models cannot avoid a universe with a beginning  Hawking and Mlodinow argue that naturalism does not need an explanation for a universe which begins to exist “ex nihilo”. A universe can be created from nothing because negative gravitational energy  cancels out positive matter energy.

On the scale of the entire universe, the positive energy of the matter can be balanced by the negative gravitational energy, and so there is not restriction on the creation of whole universes. Because there is a law like gravity, the universe can and will create itself form nothing… (Hawking and Mlodinow, 2010, p.227 )   

However, Holder notes that the fact that two properties cancel does not mean that something can pop out of nothing (Holder, 2013, p.79).  He also notes that Hawking and Mlodinow leave important questions unanswered. We can ask, why is there a law of gravity to cancel out the positive energy of matter? Furthermore, why is there a space, or space-time, on which these laws can operate? The quantum vacuum on which the laws operate is not truly nothing. It has a “rich structure which resides in a previously existing substratum of space-time” (Holder, 2004, p. 61).

A zero volume which is subject to the laws of quantum physics is not nothing: nothing means non-being. Non-being cannot have a geometrical structure; it cannot be subject to physical  laws; it cannot be described by physical  laws; it has no properties and no potentiality. Hawking  cannot answer the question “how can something come out of nothing” by treating “nothing” as something with properties.

As David Glass points out in Atheism’s New Clothes

It must be remembered that the Hartle-Hawking model is extremely speculative, but even if it is to be accepted it is far from clear that it can really support the idea that the universe had no beginning and it is also worth reiterating that it affirms that the universe is not infinitely old. Furthermore, although there are many other alternative cosmological theories that have been proposed as rivals to the big bang, none has gained widespread support and all are speculative in nature. Philosophers Bradley Monton and Graham Oppy correctly point out that we do not know all the relevant physics and so there is no guarantee that a theory of quantum gravity will include a beginning of the universe, but Monton’s claim that “we ought to conclude that it’s unknown whether there’s a big bang and hence we ought to conclude that it’s unknown whether the universe began to exist”(Monton, 2009, p.98) seems too sceptical. First, it is far from clear that alternative theories will obviate the need for a beginning and, in fact, research by Borde, Guth and Vilenkin seems to indicate that just the opposite may be the case.^[i] Second, while it can be granted that there is no conclusive proof  that the big bang theory is true or that the universe had a beginning,  the scientific evidence does strongly point in that direction.

Nor will it do to argue that it is meaningless to argue that the universe is uncaused because the term “cause” does not appear in our fundamental physics. Now, it’s true that the equations used to describe various models don’t mention causes. However, that’s not a convincing reason for thinking that there are no causes. Mathematics and the fundamental laws of physics aside, causation plays a central role in nearly every other area of human enquiry:

Causation is the most fundamental connection in the universe. Without it, there is no moral responsibility: none of our thoughts would be connected with our actions and none of our actions with any consequences…..There would be no science or technology. Any intervention we make in the world around us is premised on there being aucala connections that are to at least a degree predictable. (Mumford and Anjum, 2013, p1) 

Indeed, causation is so central that we would need very strong grounds to even consider abandoning it:

WVO Quine talked about our beliefs forming an interconnected web. All were open to revision in the light of new evidence but some of them were more central within the web. We would not easily give up our belief in logic, for instance, because it is central to everything else that we believe….A belief in causation, we would maintain, is a very central one. Nothing that occurs would have any real significance unless it was causally connected with other things….Hume even called it ‘the cement of the universe. Now, if we were to jettison causation from our web of belief, so much else would have to go with it… [i]t would require an entire reconceptualisation of the world and almost everything that we have ever believed about it. (Mumford and Anjum, 2013, p.13-14)

Such considerations lead Mumford and Anjum to reject any appeal to physics against the fundamental importance of causation:

Physics provides a representation of the world: a largely mathematical one. It is useful that it does so….But we should not forget that physics is the representation and should not be mistaken for the world itself….if we felt that physics had left out of its representation a central datum of the world – the asymmetry of causation – then we might be entitled to ask for a better physics. The world is not a number, nor an equation. It is a concrete particular inhabited by physical objects and some of them appear to be causally connected to others. Physics sometimes forces us to rethink and revise common sense, which may be perfectly legitimate. But it should not follow automatically that because a theory works out automatically within a model, the world is exactly like that model or like the maths. That is still open for debate. (Mumford and Anjum, 2013, p.12-13)

The nature of causality is primarily a philosophical question which can’t be decided by pointing to the absence of the term ’cause’ in scientific models. Some philosophers of science point out that general relativity offers a way of spelling out a scientifically precise notion of causality. It is generally taken to prohibit faster-than-light transmission of signals, for example;  we can then ask whether this notion of causality is violated by quantum mechanics. So it is perfectly meaningful and reasonable to ask “what caused the universe to exist?”

4. Hawking and the Multiverse

As mentioned above, Hartle and Hawking used Feynman’s ‘sum over histories’ formulation of quantum mechanics to describe the evolution the universe’s entire spatial geometry. Feynman’s formulation finds the probability for a certain final quantum state by a path integral, a ‘sum over histories.’ In this method, to find the probability of any particular end point one considers all the possible histories that the particle might follow from its starting point to that endpoint  a particle does not have a unique history. That is, as it moves from its starting point A to some endpoint, B, it doesn’t take one definite path but rather simultaneously takes every possible path connecting the two points (Hawking and Mlodinow, 2010, pp.96-103).

‘Sum over histories’ is usually treated as a mathematical tool, merely a method for making calculations. However, Hawking and Mlodinow interpret Feynman’s method to imply the existence of real, spatio-temporal universes with histories which differ from our own. They view all the possible states of the particle as existing ‘somewhere’ in a realised universe/multiverse. The possible alternative histories of our universe are also taken to be ontologically real, alternative  universes.  The laws of nature  and the physical constants are different for different histories.

In this view, the universe appeared spontaneously, starting off in every possible way. Most of these correspond to other universes. While some of these universes are similar to ours, most are very different… In fact, many universes exist with many different sets of physical laws. Some people make a great mystery of this idea, sometimes called the multiverse concept, but these are just different expressions of the Feynman sum over histories (Hawking and Mlodinow, 2010, p. 174-175)

Hawking and Mlodinow offer two reasons for believing in a multiverse which contains an infinite number of universes. First, they believe that this follows from Feynman’s “sum over histories” formulation of quantum mechanics. However, they do not explain how their ontological commitments follow from this convenient calculating procedure. Second, an infinitely large multiverse would explain away the appearance of design in our own universe. If the laws of nature which govern our universe had different physical constants, or if the initial conditions of the universe been slightly different, stars, galaxies and life would have been impossible. The odds of a universe which is fine-tuned for life are extraordinarily low; however, if an infinite number of universes is somehow generated, a finely-tuned universe will appear by chance alone.

Hawking and Mlodinow also argue that a “selection principle” guarantees that we observe a finely-tuned universe (2010, pp.193-197). They argue that observers can only exist in finely-tuned regions of the multiverse. It is a “scientific principle [that] the fact of our being restricts the characteristics of the kind of environment in which we find ourselves” (Hawking and Mlodinow, 2010, p. 195). So physical infinities and chance explain the existence of finely-tuned regions of the multiverse; and the “selection principle” necessarily restricts the existence of observers to finely-tuned regions. Therefore, we should not be surprised that we observe a finely-tuned universe.

However, it is not at all clear that observers could only exist in finely-tuned regions of the multiverse. A multiverse would contain “fluctuation observers” who come into being through the localised random collision of atoms (Collins, 2009, p.266). Each would be a single, isolated observer with just enough structure to have conscious experiences. The probability of such an observer assembling by chance in one region of the universe is astronomically low. However, given the probabilistic resources of an infinitely large multiverse (such as Hawking’s) there will be many more “fluctuation observers” in the multiverse than observers living in solar systems.  This is because fluctuation observers can exist in universes which have not been finely tuned for life: for example they could fluctuate into existence in the many universes with cosmological constants too large for stars or galaxies to form.

Granted, finely tuned universes can contain many more observers than a non-finely tuned universe. However, “…the low probability of a fine-tuned universe compared with a non-fine-tuned universe would completely swamp the fact that fine-tuned universes contain more observers” (Holder, 2013, p.  149). This causes a problem for the “selection principle”: the vast majority of observers in a multiverse would be fluctuation observers.  Indeed, any observer selected at random from the multiverse is much more likely to be a fluctuation observer than an observer living on an hospitable solar system. The selection principle does not guarantee that observers will live in finely-tuned universes (Holder, 2013, p149-150). So it does not explain our observation of a finely-tuned universe.

A coherent, simple explanation will tend to avoid absurdities and paradoxes. Hawking and Mlodinow rely on physical infinities to explain the existence of finely-tuned regions of the multiverse (for example, the landscape of string theory will be reproduced infinitely many times). While an actual infinite is logically possible, it is not at all clear that an actual infinite could exist in nature. The mathematician David Hilbert conceived of a hotel with infinitely many rooms. The hotel could be filled to capacity; yet one can make room for infinitely many more guests by asking the guest in room one to move into room two, the guest in room two to move into room four and so on. All the odd numbered rooms will be free, leaving enough room for infinitely many more guests.  This sort of paradox leads some to conclude that infinitely many things cannot exist simultaneously in nature. Holder (2013, p.134) notes that George Ellis has argued that such paradoxes raise problems for multiverses. And, as Holder himself argues, a theory which does not generate paradoxes is to be preferred.

Conclusion

The arguments in Hawking’s popular writings do not fully explain the existence and order of our universe. The Hartle-Hawking model does not avoid a universe with a beginning; Hawking and Mlodinow do not give a convincing argument to back up their claim that our universe could spontaneously begin to exist without a cause. Finally, the multiverse scenario discussed in “The Grand Design” has absurd consequences, generates paradoxes and conflicts with our observations. Hawking does not remove the need for a creator; and we should seek a simpler, more powerful explanation for the existence and fine-tuning of our universe.

Bibliography

Collins, R. (2009) “The Teleological Argument: An Exploration of the Fine-Tuning of the Universe”, in Moreland and Craig ed. The Blackwell Companion to Natural Theology, Malden: Wiley-Blackwell

Craig, W. and Copan, P. (2004 ) Creation Out of Nothing Grand Rapids: Baker Academic

Craig W. and Sinclair, J. (2009) “The Kalam Cosmological Argument”, in Moreland and Craig ed. The Blackwell Companion to Natural Theology, Malden: Wiley-Blackwell

Davies, P. (2006) The Goldilocks Enigma,  London: Penguin

Hawking, S. (1976) “Breakdown of Predictability in Gravitational Collapse”, Physical Review, D14

Hawking, S. (1998 ) A Brief History of Time, London: Bantam Press

Hawking, S. (2001) The Universe in a Nutshell, London: Bantam Press

Hawking, S. and Mlodinow, L.  (2010) The Grand Design, London: Bantam Books

Holder, R. (2004) God, the Multiverse, and Everything, Aldershot: Ashgate

Holder, R. (2013) Big Bang, Bigger God , Oxford: Lion

Krauss, L. (2012) A Universe from Nothing London: Simon and Schuster

Lidsey, J.E. (2000) The Bigger Bang, Cambridge: Cambridge University Press

Monton, B (2009) Seeking God in Science, Ontario: Broadview Press

Mumford, S and Anjum, R (2013) Causation: A Very Short Introduction