A shorter version of this article is available here
Scientists have increasingly become aware that the universe is ‘just right’ for life. If any one of a number of features of the universe had been even slightly different, life as we know it would be impossible. Had the ratio of the electromagnetic and gravitational forces differed by 1 part in 1060 then planets capable of supporting life could not exist. If the strong nuclear force had been weaker this would have resulted in the instability of the elements necessary for carbon-based life, while if it had been stronger this would have had a negative impact on the production of carbon and oxygen. Had the ratio of the electromagnetic and gravitational forces differed by about 1 part in 1040 then stars such as the Sun, which are capable of supporting life, could not exist. Cosmologists Stephen Hawking and Leonard Mlodinow (2010) summarize these findings:
The emergence of complex structures capable of supporting intelligent observers seems to be very fragile. The laws of nature form a system that is extremely fine-tuned, and very little in physical law can be altered without destroying the possibility of the development of life as we know it. Were it not for a series of startling coincidences in the precise details of physical law, it seems, humans and similar life-forms would never have come into being.
Philosopher Robin Collins(2009) illustrates the extent of the fine-tuning by asking us to consider the:
values of the initial conditions of the universe and constants of physics as co-ordinates on a dart board that fills the whole galaxy, and the conditions necessary for life to exist as an extremely small target, say less than a trillionth of an inch: unless the dart hits the target, complex life would be impossible.
Objections from The Multiverse
So, such “fine-tuning” has provided support for contemporary design arguments (Swinburne, 2004, pp.172-188). Perhaps the most persuasive objection to this type of contemporary design argument is to point out that our universe might just be one of many universes comprising a multiverse. If the multiverse contains a vast number of universes with different physical constants some will happen to be suitable for life just by chance. Two theoretical projects, string/M theory and eternal inflation, have led to a surge of interest in multiverse ideas (Davies, 2004). We should take some time to assess the claim that the inflationary multiverse scenario based on inflation and string theory explains the evidence of design from fine-tuning.
Inflation theory was suggested by Alan Guth in the 1980’s to deal with the “flatness problem” and the “horizon problem” (Holder, 2004, p.132). The uniformity of cosmic microwave background radiation (CMBR) creates the “horizon problem” for the classical big bang model. Temperatures throughout the universe are in every direction similar to a very high level of measurement. Distant regions of space in opposite directions to one another are causally isolated from one another. This is because the transfer of information is limited by the speed of light and the light travel time between these regions exceeds the age of the universe. Yet the fact that these different regions have evened out to a common temperature strongly suggests that they have been in causal contact with one another.
Along with the horizon problem, the classical big bang model faces the “flatness problem”. As the universe expands, the rate of expansion is slowed by the gravity of matter in the universe. In fact, the universe seems to have just enough matter to continue its expansion indefinitely. The mean density of the universe has to be just right at the very beginning to 1 part in 1060. If it was smaller than by one part in 1060 then the universe will expand much too quickly for galaxies and stars to be able to form. If the mean density was greater than one part in 1060 the whole universe would re-collapse before there had been time for stars to evolve (Lidsey, 2000, p.69-71) This means that the universe is incredibly close to having a “flat” space-time curvature.
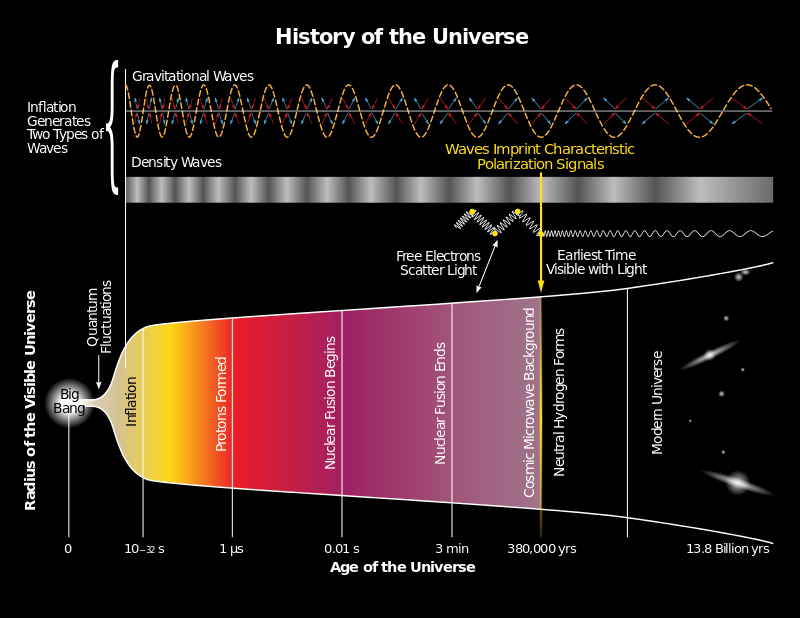
Inflation is hypothesised to account for the special initial conditions and inflation is understood as follows. According to the theory of general relativity a region of empty space will expand exponentially, unless the energy of that region of empty space was exactly zero. The gravitational effect of a field depends on the nature of the field. An electric field would cause a contraction in a region of empty space; however, so-called scalar fields cause an expansion. The negative pressure (what we normally call “tension”) in a scalar field causes negative gravitation. Guth proposed that an “inflaton field” – the name given to a scalar fieldresponsible for cosmic inflation in the very early universe – caused a very small region of space to expand exponentially, overpowering the massive force of gravity (Davies, 2006, p.67-69). The result was that the universe underwent an incredibly rapid period of accelerating expansion from 10-35 to 10-32 seconds after the origin (Holder, 2013,p.119).
During this infinitesimally small fraction of a second the universe expanded from 10-25 cm to 10 metres across; then the slower deceleration described by the classical Big Bang theory took over. Guth suggested that the inflaton field was inherently unstable and would have decayed after 10-32 seconds. The enormous energy stored in the inflaton field during the inflationary phase was converted into the heat energy of the Big Bang. But since E=mc2 , it was possible for this heat energy to be converted into the 1050 tonnes of matter in the observable universe (Davies, 2006, p.70). The “flatness” and the “horizon” problems disappear on the inflationary hypothesis. The horizon problem is solved because there would be enough time for light to travel from one region to another before the period of rapid expansion. The flatness problem disappears because the rapid, exponential expansion of the inflation era had the effect of “flattening out” curvature. (Lidsey, 2000, pp.77-79).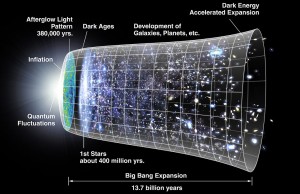
However, there was a flaw in Guth’s scheme: because the decay of the inflaton field is a quantum process the decay forms randomly distributed “bubbles” of space. The “bubbles” into which the inflaton field had decayed would be surrounded by regions of space where the inflaton field had not decayed. The energy given up by the decayed inflaton field would be concentrated in the “bubble walls”; bubble collisions would release this energy as heat, and such a chaotic process would not create the isotropic and homogenous universe which we observe (Davies, 2006, pp.70-71).
To solve this problem, Linde and Vilenkin proposed the theory of “eternal inflation”. An eternally inflating universe consists of an expanding ‘sea’ of false vacuum which is constantly spawning ‘island universes’ like ours (Vilenkin, p.170). Because the inflaton field is subject to quantum uncertainty it will fluctuate randomly and spontaneously in different times and spaces. In some places and at some times the field undergoes a strengthening fluctuation, which causes the rate of inflation to increase. Most fluctuations are too small to override the decay of the inflaton field; however inflation causes space to expand exponentially. There will always be regions of space that continue to inflate, and these represent the greater part of the volume of physical space. The universe is dominated by inflating space interspaced with ‘island universes’ which have ceased inflating and are expanding at a decelerating rate. Indeed, because inflation never stops the production of new ‘island universes’ is a never-ending process.
Eternal inflation delivers a (potentially) infinitely large, “patchwork” multiverse. However, to explain away fine tuning we need some ‘mechanism’ to account for the variation of the constants of nature. The process of “symmetry breaking” could explain why different regions of the universe have different physical constants. Symmetry is “invariance under a specified group of transformations” (http://plato.stanford.edu/entries/symmetry-breaking/#1); or, as Sean Carroll explains, it is “a situation where you can rearrange things a bit (values of quantum fields, positions in space, any of the characteristics of some physical state) and get the same answer to any physical question you may want to ask.” (http://blogs.discovermagazine.com/cosmicvariance/2005/10/24/hidden-symmetries/#.U0bYCPldXfI)
Symmetry breaking is explained by Davies as follows: “High temperature systems manifest more symmetry than low temperature systems. When the temperature falls, symmetries get broken” (Davies, 2006, p.182). The more symmetry a system possesses, the less structure and complexity. Symmetry decreases with temperature; so the universe had a high degree of symmetry in the aftermath of the Big Bang. As the universe cooled more symmetries became broken as more structure and complexity emerged. Conceivably, the values of the undetermined parameters of the Standard Model could have resulted from these symmetry decreasing phase transitions.
We can use the electroweak force to illustrate how symmetry breaking occurs. At temperatures above 1015 degrees the weak force had the same long range as the electromagnetic force. The W and Z particles which are exchanged to convey the weak force, have a very short range due to their large masses. Subatomic particles gain their mass by interacting with the Higgs field. At temperatures above 1015 degrees (the temperature of the electroweak phase transition) the Higgs field averages to zero. At this temperature, then, the W and Z particles were massless. This gave the weak force the same range as electromagnetism (which is conveyed by photons, which also have a mass of zero.) As the temperature drops the Higgs field breaks symmetry and its strength jumps to a very large non-zero value (Davies, 2006, p.188).
During the GUT era, before 10-36 seconds, the universe would have had a temperature of 1024 degrees and the strong and weak nuclear forces were combined. As the universe cooled both the form and nature of matter, and the effective low energy laws, would have become more complex and differentiated (Davies, 2006, p.189). As a result of this process, different domains might end up with very different particle masses and force strengths. Furthermore, there might be other ways of breaking symmetries which lead not only to different constants, but different forces entirely. The inflation era is the era when many theorists believe that three of the fundamental forces were united: the strong and the weak nuclear force and the electromagnetic force. The strong and the weak forces emerged at the end of the inflationary period and the electromagnetic and weak nuclear force emerged around 10-10 seconds.
String theory attempts to unify the fundamental forces of nature on the Planck scale – which applies to 10-43 seconds from the universe’s origin. At this scale a theory must be able to combine gravity with the other fundamental forces. String theory postulates that one dimensional objects known as strings, some 10-33cm across, are the ultimate constituents of the physical universe. The elementary particles are different modes of the strings’ vibration. These vibrations occur in more than three dimensions. M-theory, a development of string theory, theorises that there are 11 dimensions. The reason we can only detect three is that the other 8 are “curled up very small, leaving three dimensions which are large and nearly flat” (Hawking, 2001,p.88) in a process known as compactification. The laws of nature that we observe depend on the way in which the extra dimensions “curl up”.
Compactification is string theory’s version of symmetry breaking. For example, a simple symmetric shape such as a big, six-dimensional sphere might shrivel spontaneously into a complicated, multi-dimensional labyrinth of twisted bridges and bifurcating tunnels….The key point here is that the laws of physics that apply in the remaining (uncompactified) space depend on the specific shape of the compactified dimensions. In string/M theory the low energy physics of the three dimensional world we observe is determined by the particular shape of the compactified extradimensions (Davies, 2006, p.190-191, emphasis in original).
On some estimates, the compactification process described by string theory allows for a landscape of 10500 low energy universes. Eternal inflation provides a mechanism for populating that landscape. In eternal inflation, as we have noted, the overall matrix of inflating space has no end. The nucleation events which lead to the formation of “pocket” universes are quantum mechanical in nature; therefore there will be variation in the compactification process in each “pocket”. Inflation is never-ending, so there is sufficient time for it to bring about every possible low-energy world.
Multiverses By Design
If true, would the combination of eternal inflation and string-theory explain away the need for a designer? This seems unlikely; as Holder notes the multiverse itself would require fine tuning (Holder, 2004, p.141). For example, the inflationary multiverse’s overall mean density must be less than or equal to the critical value which gives rise to a flat space-time, so that the inflationary multiverse as a whole is infinite and expands forever. In principle the density can take any value from an enormously large range; if it is greater than the critical value the resulting universe will be finite (Holder, 2012, p.142-144)
Robin Collins notes that the correct combination of laws and fields must be in place for the inflationary-type multiverse generator to explain the fine-tuning of the constants: this particular process of multiverse-generation itself required fine tuning. Without an inflaton field to give empty space a positive energy density, a small region of space would not expand into a large region. Einstein’s General Theory of Relativity is also essential to this expansion because it dictates that space will expand at an enormous rate in the presence of a large near-homogeneous positive energy density.
Furthermore, we need some ‘mechanism’ to account for the variation of the constants of nature. The combination of inflationary cosmology with superstring/M-theory allows for 10500 possible combinations of the laws of physics. GUT’s other than string theory only allow for a small number of combinations – so if string theory was not true, and another GUT was true, the inflationary multiverse would not produce the necessary variation in the constants of nature in each “island universe”. Finally, and crucially, the fundamental laws underlying multiverse generation must be just right. Without the Principle of Quantization all electrons would fall into the atomic nuclei; without the Pauli Exclusion Principle, electrons could only occupy the lowest atomic orbit and complex chemistry would be impossible; without gravity, planets and stars could not exist.
Roger Penrose has pointed out that inflation itself is highly improbable; therefore, it does not solve the problem of the universe’s highly ordered initial conditions (Holder, 2012, p.123). Order can be measured by a quantity called entropy (very roughly, the lower the order the higher the entropy) and the second law of thermodynamic demands that the entropy of the universe always increases – indeed, because inflation is a thermalization process it will certainly be entropy increasing (Collins, 2012, p. 250). Therefore the pre-inflationary patch of space-time must have had a lower entropy than the universe right after inflation; inflation requires special low-entropic initial conditions to explain the special conditions of the Big Bang. These low-entropic initial conditions would be examples of fine-tuning in need of explanation.
To gain a sense of the level of fine-tuning required, note that Penrose calculates that the entire solar system with all its planets and all its inhabitants could be created by the random collisions of particles and radiation with a probability of 1 in 1010^60 . Penrose also calculates that the order of our universe exceeds this by an astonishing degree: there are something like 1010 ^123 possible universe configurations, only one of which would have the order of our universe. The pre-inflationary patch of space-time must have lower entropy than the universe after inflation; therefore, there was a high degree of order present in the universe’s initial conditions. (Holder, 2013, p.144-145).
The multiverse proponent could attempt to account for the extraordinary order of the universe’s starting configuration by arguing that that there are infinitely many universes, covering every possible starting configuration. However, we only require enough order for one solar system to support a community of intelligent observers. It follows that our universe has vastly more order than is required for our existence. But, if the multiverse hypothesis is true there is no reason to think that our universe is anything but a typical member of the set of habitable universes. We should find ourselves in a universe which is “marginally biophilic” and not a universe with vastly more order than that required for our existence:
A general feature of random processes is that big flukes are much rarer than little flukes…Therefore if human beings are just arbitrary, random observers among all possible observers, then we are far more likely to find ourselves living in a universe only marginally bio-friendly than one which is optimally bio-friendly, simply because there are many more of the former than the latter. (Davies, 2006, p.198)
At a fundamental level, then, the mystery of fine-tuning would remain. This particular multiverse hypothesis still requires fine-tuning of the initial conditions and the laws of nature. Indeed, Swinburne points out that to produce life a universe needs a large number of particles of few kinds with forces of some complexity acting between them. Of all the logically possible worlds, very few will have multiverse generating mechanisms which will inevitably produce a life-supporting universe (Swinburne, 2004, p. 186-188). So such a multiverse generating mechanism will stand in need of explanation.
But is there a Multiverse?
If true, the combination of eternal inflation and string theory would not explain away the need for a designer. Yet we might want to ask if such a multiverse generator really exists. Even if the detection of gravitational waves by BICEP2 support the cosmic inflation theory ( http://news.stanford.edu/news/2014/march/physics-cosmic-inflation-031714.html) these results do not confirm the existence of a multiverse which would explain fine-tuning. Whether or not inflation produces a multiverse depends on the properties of the initial field responsible for inflation.
We should also note that string theory is highly speculative. Quantum gravity effects can only become apparent at extraordinarily high energies. We would need accelerators at least 10 light years’ in length to do experiments at these levels (Holder, 2004, p.23). It does not seem possible to confirm string theory experimentally. Indeed, even as Lawrence Krauss uses the inflationary multiverse scenario to explain away the appearance of design, he cautions the reader that we do not know, and may never know, if string theory is true (Krauss, 2013, pp 130-135)! This is significant, because the scientific method was founded on the assumption that the laws of nature were contingent; philosophers could not deduce the truth about nature by abstract reasoning. Observation and experimentation were essential to discovering the truth about the natural world (Hannam, 2009, p.340). Arguably, string theory has the virtues of simplicity, elegance and beauty; but if theorists lose all contact with observation and experiment we might wonder if string theory is more akin to metaphysics (making this multiverse model “fair game” for philosophical critique).
Hawking and Mlodinow’s Multiverse
Stephen Hawking has used Feynman’s ‘sum over histories’ formulation of quantum mechanics to describe the evolution the universe’s entire spatial geometry. Feynman’s formulation finds the probability for a certain final quantum state by a path integral, a ‘sum over histories.’ In this method, to find the probability of any particular end point one considers all the possible histories that the particle might follow from its starting point to that endpoint a particle does not have a unique history. That is, as it moves from its starting point A to some endpoint, B, it doesn’t take one definite path but rather simultaneously takes every possible path connecting the two points (Hawking and Mlodinow, 2010, pp.96-103).
‘Sum over histories’ is usually treated as a mathematical tool, merely a method for making calculations. However, Hawking and Mlodinow interpret Feynman’s method to imply the existence of real, spatio-temporal universes with histories which differ from our own. They view all the possible states of the particle as existing ‘somewhere’ in a realised universe/multiverse. The possible alternative histories of our universe are also taken to be ontologically real, alternative universes. The laws of nature and the physical constants are different for different histories.
In this view, the universe appeared spontaneously, starting off in every possible way. Most of these correspond to other universes. While some of these universes are similar to ours, most are very different… In fact, many universes exist with many different sets of physical laws. Some people make a great mystery of this idea, sometimes called the multiverse concept, but these are just different expressions of the Feynman sum over histories (Hawking and Mlodinow, 2010, p. 174-175)
Hawking and Mlodinow offer two reasons for believing in a multiverse which contains an infinite number of universes. First, they believe that this follows from Feynman’s “sum over histories” formulation of quantum mechanics. However, they do not explain how ontological commitments follow from this convenient calculating procedure. Second, an infinitely large multiverse would explain away the appearance of design in our own universe. If the laws of nature which govern our universe had different physical constants, or if the initial conditions of the universe been slightly different, stars, galaxies and life would have been impossible. The odds of a universe which is fine-tuned for life are extraordinarily low; however, if an infinite number of universes is somehow generated, a finely-tuned universe will appear by chance alone.
Hawking and Mlodinow also argue that a “selection principle” guarantees that we observe a finely-tuned universe (2010, pp.193-197). They argue that observers can only exist in finely-tuned regions of the multiverse. It is a “scientific principle [that] the fact of our being restricts the characteristics of the kind of environment in which we find ourselves” (Hawking and Mlodinow, 2010, p. 195). So physical infinities and chance explain the existence of finely-tuned regions of the multiverse; and the “selection principle” necessarily restricts the existence of observers to finely-tuned regions. Therefore, we should not be surprised that we observe a finely-tuned universe.
However, it is not true that observers could only exist in finely-tuned regions of the multiverse. A multiverse would contain “fluctuation observers” who come into being through the localised random collision of atoms (Collins, 2009, p.266). Each would be a single, isolated observer with just enough structure to have conscious experiences. The probability of such an observer assembling by chance in one region of the universe is astronomically low. However, given the probabilistic resources of an infinitely large multiverse (such as Hawking’s) there will be many more “fluctuation observers” in the multiverse than observers living in solar systems. This is because fluctuation observers can exist in universes which have not been finely tuned for life: for example they could fluctuate into existence in the many universes with cosmological constants too large for stars or galaxies to form.
Granted, finely tuned universes can contain many more observers than a non-finely tuned universe. However, “…the low probability of a fine-tuned universe compared with a non-fine-tuned universe would completely swamp the fact that fine-tuned universes contain more observers” (Holder, 2013, p. 149). This causes a problem for the “selection principle”: the vast majority of observers in a multiverse would be fluctuation observers. Indeed, any observer selected at random from the multiverse is much more likely to be a fluctuation observer than an observer living on an hospitable solar system. The selection principle does not guarantee that observers will live in finely-tuned universes (Holder, 2013, p149-150). So the combination of a selection principle with a multiverse does not explain why we observe a finely-tuned universe!
Other observations tell against the Hawking/Mlodinow Multiverse. As we noted when discussing the inflationary multiverse, if our universe is just one biophilic “bubble” in a multiverse, it is probable that it would only be marginally biophilic (a “little luck” will be much more common than a “lot of luck”; marginally biophilic regions will be much more common in an infinitely large multiverse than those which are optimally biophilic). Yet our universe seems optimally bio-friendly in several respects. The lifetime of the proton is at least 2 x 1032 years, which is at least 1022 times the age of the universe. The longevity of the proton vastly exceeds that necessary for the existence of life (Holder, 2013, p.145). The measured value of the cosmological constant is one tenth of the value above which galaxies would not form (Davies, 2006, p.199). Holder notes that this factor of ten seems to be “a bit too special”. Indeed, he notes that Paul Davies considers the value of the cosmological constant to be “optimal” for biological life (Holder, 2013, p.141).
Finally, we should note that a coherent, simple explanation will tend to avoid absurdities and paradoxes. Hawking and Mlodinow rely on physical infinities to explain the existence of finely-tuned regions of the multiverse (for example, the landscape of string theory will be reproduced infinitely many times). While an actual infinite is logically possible, it is not at all clear that an actual infinite could exist in nature. The mathematician David Hilbert conceived of a hotel with infinitely many rooms. The hotel could be filled to capacity; yet one can make room for infinitely many more guests by asking the guest in room one to move into room two, the guest in room two to move into room four and so on. All the odd numbered rooms will be free, leaving enough room for infinitely many more guests. This sort of paradox leads some to conclude that infinitely many things cannot exist simultaneously in nature. Holder (2013, p.134) notes that George Ellis has argued that such paradoxes raise problems for multiverses. And, as Holder himself argues, a theory which does not generate paradoxes is to be preferred.
Theism, Naturalism and Scientific World-views
We have no strong reason to believe that the inflationary multiverse scenario is true. Even if we did have reason to believe it was true, it would merely raise the question of how the multiverse came about in such a way as to make life inevitable. Inflation seems to require fine-tuning. The inflationary multiverse scenario also requires a number of components to be in place- the correct laws and initial conditions – without any one of which it would still almost certainly fail to produce a single life-sustaining universe. Therefore the inflationary multiverse scenario does not explain away the evidence for design.
Finally, the multiverse scenario discussed in “The Grand Design” has absurd consequences, generates paradoxes and conflicts with our observations. Hawking does not remove the need for a creator; and we should seek a simpler, more powerful explanation for the fine-tuning of our universe. According to the design argument, the best explanation is that the universe is the product of a rational mind. The basic motivation for design can be expressed as follows. We consider a range of possible values for these features of the universe and then ask why they happen to have values lying in the very precise region suitable for life. From an atheistic perspective, there seems to be no reason for this whatsoever. That is, given only atheism and our current scientific knowledge we would have no reason to expect the values of these features to be in the life-permitting range.
By contrast theism provides a very neat explanation. Fine-tuning is a very precise example of the sort of order we’d expect to find in a universe created by God. God would have reason to bring about valuable things, like the remarkable beauty of a highly structured universe. In light of this, we’d have reason to expect God to create a universe that is fine-tuned with values in the life-permitting range. In other words, fine-tuning is the sort of thing we’d expect in a theistic universe, but not at all what we’d expect in an atheistic universe. As such, it provides strong evidence in favour of the existence of God.
There are several common objections to this argument. One is based on the anthropic principle, which is the idea that we shouldn’t be surprised to observe a fine-tuned universe because if it wasn’t fine-tuned we wouldn’t be here to observe it. At one level this seems right – we could only observe a fine-tuned universe – but this doesn’t undermine the design argument. The existence of observers does not explain the fine-tuning of the universe; rather, the existence of intelligent observers is itself a surprising fact in need of explanation. The design argument provides an explanation why the universe is fine-tuned in the first place and hence why the existence of intelligent life is even possible. From an atheistic perspective, there’s no good explanation for fine-tuning and so no good explanation for the existence of intelligent life. It’s generally agreed that the anthropic objection to the fine-tuning argument fails.
Another objection suggests that future science will provide an explanation for fine-tuning in terms of a more fundamental law, a theory of everything perhaps. Now if such an alternative explanation were available proponents of the fine-tuning argument would certainly have to respond. However, in the absence of such an explanation, the mere possibility that one might turn up in the future is cannot explain away design. In fact, it seems like wishful thinking on the part of opponents of the fine-tuning argument. Indeed, the best current candidate to account for the laws and constants of physics, M-theory, does not predict them uniquely, but allows for numerous possibilities. Finally, even if a new theory did account for the fine-tuning evidence, it would just push design back to the level of the theory because it would raise the question of why this particular theory, i.e. one that describes a universe suitable for life, is the theory that applies to the actual universe.
Several further objections claim that theism doesn’t provide a good explanation. One reason given for this is that we don’t know what sort of universe God would want to bring about. However, God and humans have certain properties in common. Both are rational, both are agents, and -unless we wish to embrace some form of moral scepticism – we should acknowledge that both would recognise similar values. We know from observation and our own direct experience that rational agents bring about complex states of affairs that are ordered for some purpose (eg. machines) or that bring about some value (eg art). The objective beauty of the cosmos, and the fact it makes biological life possible, cry out for a theistic explanation.
We must compare God’s reasons for creating a fine-tuned universe with the absence of any reason for a finely tuned universe given atheism. The point is that this complex and valuable state of affairs is much, much more likely given theism than chance. So some atheists turn to another objection: theism doesn’t provide a mechanism to explain how fine-tuning came about. However, it is perfectly possible to have good explanations that don’t provide a mechanism. If humans were ever to find a complex artefact on a distant planet, it would be very reasonable to infer intelligent agency even if we had no idea what sort of mechanism was produced the artefact.
It must be stressed that theism provides a personal rather than scientific explanation and personal explanations appeal to beliefs and intentions rather than specifying precise mechanisms (see God and Agent Explanations: a Guide for the Perplexed). And even in a science such as physics, mechanisms are not nearly as important as is often assumed. Isaac Newton’s theory of gravity, for example, provided powerful explanations of planetary motion even though there was much disagreement about the mechanism by which one massive body exerted a force on another. The same applies in quantum theory; no-one really knows what’s going on, but quantum theory certainly explains a lot!
But isn’t God too strange or too remote or too improbable to be considered as a reasonable explanation? We’ve dealt with Richard Dawkins’ argument that God is improbable elsewhere (here,here and here), but it’s worth making a few general points. First, in science, a hypothesis shouldn’t be effectively ruled out just because it doesn’t match our previous experience – the key question is whether the evidence is what we’d expect. If this applies in science, why apply different rules in this context? Second, theism is a very clear and simple hypothesis. The creator is single being who is unlimited in power, knowledge and goodness. The terms used to describe God are pellucid. It might be difficult to imagine an infinite series or a billion sided shape. That does not mean that the terms are difficult to understand!
Third, theism appeals to a kind of explanation we are familiar with – personal explanation. Of course, there are differences between God and human agents, but theism relates to one of the two main kinds of explanation (personal and scientific). Fourth, theism might seem odd to some people, but when we are talking about the fundamental nature of reality some things are going to be odd (just look at modern physics!)
Finally, we must not make the mistake of comparing theism to a cosmological model. As should be obvious from our discussion of the inflationary multiverse, theism is compatible with many cosmological models. Indeed, early scientists stressed the importance of observation and measurement precisely because we cannot predict the design that God would use to create the universe from our arm chairs. We need to examine the universe by observation and measurement to see how God created the world.
In fact, we are comparing the rationality of naturalism and theism, neither of which is a scientific model. Naturalism and theism are worldviews. Each has a scope much wider and deeper than any scientific model or theory. For example, each asks questions like: “why does the observable world behave with such law-like regularity?”; “why can we describe the world using mathematical models?”; “is there more to the world than the quantifiable and observable?” Simply asking these questions reveals that they cannot be answered with a mathematical model.
Indeed, naturalism is notoriously difficult to define. At its roots it contends that “nature” is all that exists. Beyond that, things get murkier. What exactly do we mean by “nature”? Can a naturalist believe that consciousness is an emergent state, radically unlike anything that exists in physics or biology? Can naturalism allow that moral and aesthetic values exist in some Platonic realm? The jury is out. Naturalists – like everyone else – have discovered an ordered, comprehensible universe which they can describe with mathematical models. But that does not mean that naturalism explains or predicts such a universe. There is no good reason to expect an un-designed and purposeless universe to exhibit order, structure and regularity. In other words, naturalism struggles to provide a deep, robust and satisfying explanation of fine-tuning.
Bibliography and Further Reading
Collins, R. (2009) “The Teleological Argument: An Exploration of the Fine-Tuning of the Universe”, in Moreland and Craig ed. The Blackwell Companion to Natural Theology, Malden: Wiley-Blackwell
Davies, P. (2004) “Multiverse Cosmological Models” Modern Physics Letters, A Vol. 19, No. 10: 727–743
Davies, P. (2006) The Goldilocks Enigma, London: Penguin
Hannam, J. (2009) God’s Philosophers, London: Icon
Hawking, S. (2001) The Universe in a Nutshell, London: Bantam Press
Hawking, S. and Mlodinow, L. (2010) The Grand Design, London: Bantam Books
Holder, R. (2004) God, the Multiverse, and Everything, Aldershot: Ashgate
Holder, R. (2013) Big Bang, Big God, Oxford: Lion
Krauss, L. (2012) A Universe from Nothing London: Simon and Schuster
Lidsey, J.E. (2000) The Bigger Bang, Cambridge: Cambridge University Press
Polkinghorne, J. and Beale, N. (2009) Questions of Truth, Kentucky: Westminster John Knox Press
Swinburne, R. (2004) The Existence of God, Oxford: Oxford University Press
[1] Victor Stenger has objected to the scientific consensus on fine-tuning. See, for example, hisThe Fallacy of Fine-Tuning: Why the Universe is Not Designed for Us. Prometheus Books, 2011. For responses, see the article by Robin Collins, ‘Stenger’s Fallacies’http://home.messiah.edu/~rcollins/Fine-tuning/Stenger-fallacy.pdf and another article by Luke Barnes, ‘The Fine-Tuning of the Universe for Intelligent Life’http://arxiv.org/PS_cache/arxiv/pdf/1112/1112.4647v1.pdf